So I was trying to practice for some interviews with some gaming studios. I read on GlassDoor.com that one of the companies I had an interview for would ask about Tree Traversal methods. Upon doing some research I found multiple websites mentioning Depth First Search and Breadth first search.
I learned that there are essentially a few rules to DFS (Depth First Search).
- Depth first search goes all the way down one side of the tree first, and then moves left to right.
- For each node, we will add it to the array
- For each child node, we will call the depth first search method to add the children to the array
For example, given the tree :
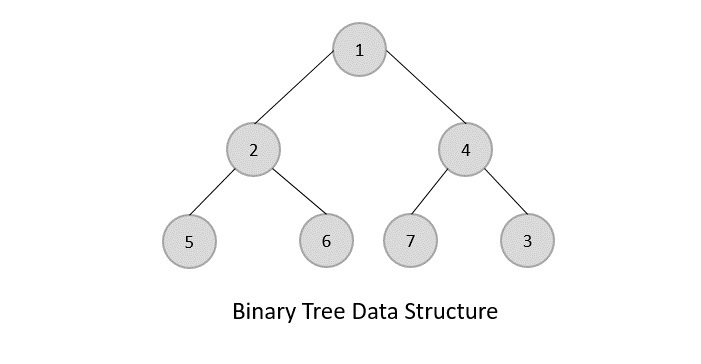
The algorithm will first go down the left side, look at the root, it will start at letter A, and then move left to B, add A and B to the array of elements. After this, it will go down to D, and check all the nodes on D. The new array would look like: [A,B,D] and then it will look at it’s left and right child nodes, and add them. The new array would look like: [A,B,D,H,I] so essentially the rule is, add the elements and then check the children, and add the children, recursively.
So I came up with a super duper simple method of doing this:
void dfs(Node* node, vector<int>& levelOrder)
{
if (node == nullptr)
return;
levelOrder.push_back(node->data);
dfs(node->left, levelOrder);
dfs(node->right, levelOrder);
}Essentially, it’s using a recursive method to first check that the incoming node is not a nullptr. If it’s not a null pointer, we then add the node’s data element to the incoming vector, and then call the dfs method on both the left and right nodes.
I just wanted to mention that in a recursive function like this, you can have a stack overflow if the depth of the tree is too large. This is just something to be aware of.
BST Traversal
There’s actually there different methods of traversing a binary search tree. The first one that I posted above is essentially root, left, right. This is just a pre-order traversal.
There’s actually three in total, and they all are essentially just different places where we put the root node.
The three are called:
Preorder Traversal
Postorder Traversal
Inorder Traversal
This is very simple honestly. In order is literally “in order”, left, root, right.
It could be implemented like this:
void inOrderTraversal(BST* tree, vector<int> &array)
{
if (tree)
{
inOrderTraversal(tree->left, array);
array.push_back(tree->value);
inOrderTraversal(tree->right, array);
}
}If you notice, it’s literally the same as the above pre-order traversal but we change the order of when we call the recursive methods. If you notice, first we call the method on the left of this tree, then we add “this” to the array, and finally we call it again on the right. So if you imagine it, it’s going to essentially add the inputted tree’s value to the array, after adding the left node, then it will add the root and finally the right node’s value. It’s a bit tricky but I hope that makes sense.
Pre Order is the version all the way at the top, so now, I’m going to go over postorder.
void postOrderTraversal(BST* tree, vector<int> &array)
{
if (tree)
{
postOrderTraversal(tree->left, array);
postOrderTraversal(tree->right, array);
array.push_back(tree->value);
}
}If you notice, the only thing that changed is now we are basically going to add the left and right nodes first, and then finally the root node.
I think the best way to think about this is to take a large tree, and split it into it’s sub-trees and think of them separately and imagine how this method would work if called on a single 3 node tree with a root, left and right node.
I hope this helps other people who are studying.
